Rotate and reflect video and images
Orientation and symmetry of static images or frames displayed during a real time playback of video streams can be changed using "Rotate and reflect" operations.
Rotation and reflection are specific types of general 2-dimensional transformation (2D Transform) of image. It is frequently used together with the "Zoom (magnify)" 2D transform operations.
Zooming can be initiated using the following user interface elements:
Major types of "Rotate and reflect" operations and symmetry modes are shown in the Table 1.
| Operation | Symmetry mode | Transform | User access |
|---|---|---|---|
| Rotate right 90° | Rotate right 90° | 1 ➔ 7 |
Menu |
| Rotate left 90° | Rotate left 90° | 1 ➔ 3 |
Menu |
| Rotate 180° | Rotate 180° | 1 ➔ 5 |
Menu |
| Reflect vertical | Reflect vertical | 1 ➔ 8 |
Menu |
| Reflect horizontal | Reflect horizontal | 1 ➔ 4 |
Menu |
| Reflect in diagonal y = x | Reflect in diagonal y = x | 1 ➔ 2 |
Menu |
| Reflect in diagonal y = -x | Reflect in diagonal y = -x | 1 ➔ 6 |
Menu |
| No Transform (Identity) | No Transform (Identity) | 1..8 ➔ 1 |
Menu |
| Restore original mode | Restore original mode | 1..8 ➔ 1..8 | "Rotate and reflect" dialog |
| Custom rotate and reflect | Custom rotate and reflect | 1..8 ➔ 1..8 |
Menu "Rotate and reflect" dialog |
Symmetric and non-symmetric transformations of image
Image can be rotated by arbitrary angle and reflected in mirror plane placed in arbitrary direction relative x-y coordinate system of image's plane.If the same 2D transformation or a different one is applied multiple times, there are possible two very different situations:
- Transformed image never coincides with itself
- Transformed image coincides with itself at some step of transformations.
There exists an infinite number of different rotate and reflect 2D transformation. Only a few of them can be characterized as symmetric. A sub-group of symmetric transformation often used in image and video processing is presented in the Table 1. It includes rotation by 90° (left and right), rotation by 180°, reflection in horizontal, vertical, and diagonal (x = y and x = -y) mirror planes.
A diagram shown in Figure 1 explains how these elementary symmetric 2D transformations convert image from one "standard" position to another. Standard position "1" is considered as an "Identity" or "no transformation", and corresponds to the not transformed original image.
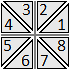 Figure 1.
Standard positions of elementary symmetric 2D transformations.
Figure 1.
Standard positions of elementary symmetric 2D transformations.
The column titled "Transform" in the Table 1
shows how a triangle placed in the standard position "1" is modified, rotated or reflected, by these elementary transformations.
These operations can be initiated via the main menu, pop-up menu of video pane and "Rotate and reflect" dialog.
Rotate right 90° (1 ➔ 7)
Rotate clockwise (from left to right) all points of image about the z axis perpendicular to the xy plane of image by 90°.
Rotate left 90° (1 ➔ 3)
Rotate counter clockwise (from right to left) all points of image about the z axis perpendicular to the xy plane of image by 90°.
Rotate 180° (1 ➔ 5)
Rotate all points of image about the z axis perpendicular to the xy plane of image by 180°.
Reflect vertical (1 ➔ 8)
Reflect all points of image in the mirror plane placed "horizontally". That mirror plane is perpendicular to the xy plane of image, and intersects xy plane along x axis.
Reflect horizontal (1 ➔ 4)
Reflect all points of image in the mirror plane placed "vertically". That mirror plane is perpendicular to the xy plane of image, and intersects xy plane along y axis.
Reflect in diagonal y = x (1 ➔ 2)
Reflect all points of image in the mirror plane x = y in the xy plane of image. That mirror plane is perpendicular to the xy plane of image, and intersects xy plane along the diagonal line y = x.
Reflect in diagonal y = -x (1 ➔ 6)
Reflect all points of image in the mirror plane x = -y in the xy plane of image. That mirror plane is perpendicular to the xy plane of image, and intersects xy plane along the diagonal line y = -x.
No Transform (Identity) (1..8 ➔ 1)
Transform an image from the current state to the "Identity" (No Transform) state. Image is returned to the original state which it had before any previous transformations were applied.
Restore original mode (1..8 ➔ 1..8)
Transform an image from the current state to the state which it had when "Rotate and reflect" dialog was just open. This operation is available only from the "Rotate and reflect" dialog.
Custom rotate and reflect (1..8 ➔ 1..8)
These operation opens "Rotate and reflect" dialog.From this dialog image can be transformed by applying a single or multiple elementary operations at once. In the single elementary operation mode (instant update), an image is updated instantly after invoking each elementary operation. In the combine operation mode (non-instant update), several operations are sequentially combined in a group, and the whole group transformation is applied at once. It is done by clicking the button "Apply" in the "Rotate and reflect" dialog.